|
Pipo Prods.
| ||||
|
| ||||
|
Analyse spectrale - méthodes paramétriques
Cet article est destiné à une lecture en ligne sur votre écan, si vous souhaitez l'imprimer, téléchargez la version PDF.
Introduction
Les méthodes paramétriques d'analyse spectrale nécessitent une connaissance a priori sur les caractéristiques du signal (allure générale de son spectre). Elles permettent de dresser un modèle mathématique du signal à partir des coefficients d'un filtre. Pour illustrer ces méthodes, un signal d'électroencéphalogramme (EEG) va être analysé puis modélisé.
Analyse non-paramétrique
Le signal est, dans un premier temps, analysé avec des méthodes non paramétriques (périodogrammes) permettant d'avoir l'a priori nécessaire pour le modéliser.
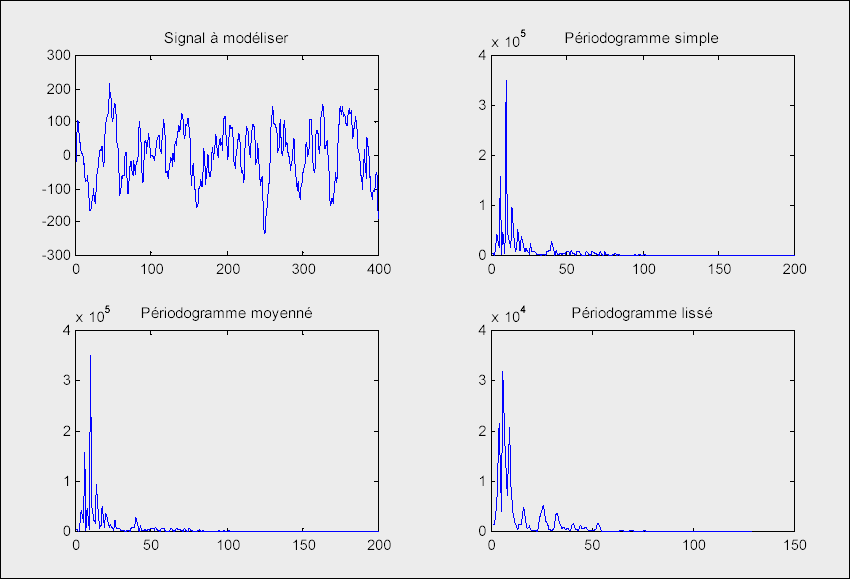
Analyse non paramétrique du signal EEG
Cette première analyse permet de déterminer les méthodes paramétriques à utiliser. Ce signal est constitué de composante fréquentielles dominantes (pics fréquentiels). On peut dores et déjà prévoir qu'un modèle autorégressif (AR) permettra de modéliser au mieux ce signal. Le modèle moving average (MA) étant plus adapté à la modélisation de signaux dont le spectre est assez plat, son utilisation sur un tel signal ne donnera pas de bons résultats. Ces deux modèles paramétriques vont être testés sur le signal EEG afin de vérifier ces affirmations.
Analyse paramétrique
La modélisation d'un signal par des techniques paramétriques nécessite une intervention humaine sur le modèle. Il faut, dans un premier temps, définir le modèle le mieux adapté au signal à modéliser. Une fois le modèle choisi, il faut déterminer son ordre, c'est à dire le nombre de coefficients permettant au mieux de modéliser ce signal. Le choix du modèle se fait en général en fonction de l'allure du spectre, mais l'ordre du modèle ne peut pas être déterminé précisément sans une analyse plus fine. Le choix de l'ordre se fait en général en minimisant un certain critère d'erreur entre le signal en sortie du modèle et le signal mesuré.
Pour chacun des deux modèles étudiés, quatre critères d'erreur sont minimisés, les critères d'Akaike, MDL, Final Prediction Error et Parzen. Ces quatre critères sont ne sont pas uniques, chaque cas peut nécessiter la minimisation selon un critère personnel en fonction des contraintes.
Modèle autorégressif (AR)
Principe
Un modèle autorégressif est un filtre tout-pôle (composé uniquement de pôles) au travers duquel passe un bruit blanc. On détermine les coefficients de ce filtre tels que le signal à sa sortie soit le plus proche possible du signal à modéliser.
Fonction de transfert
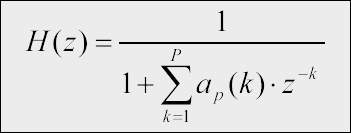
La sortie d'un tel filtre dépend des échantillons précédents de la sortie et de l'échantillon actuel du bruit. Les coefficients ap(k) agissent uniquement sur les échantillons précédents de la sortie.
Fonction Matlab
La fonction suivante calcule les coefficients d'un modèle autorégressif en minimisant l'un des quatre critères donnés précédemment. La méthode de calcul est la résolution de l'équation de Yule Walker par l'algorithme de Levinson. Trois modes sont possibles :
Minimisation de l'erreur, choix de l'ordre
L'évolution de l'erreur est étudiée selon les quatre critères (premier mode de fonctionnement de la fonction).

Evolution des différents critères d'erreur
On remarque que, selon le critère choisi, l'erreur n'évolue pas de la même façon (la courbe est plus ou moins plate). On remarque également que l'ordre optimal pour le modèle varie d'un critère à l'autre.
Modélisation du signal EEG
Pour la visualisation du comportement du modèle, le critère d'erreur choisi est le critère d'Akaike. L'ordre du modèle autorégressif est donc 12, le modèle comporte 13 coefficients.

Représentation temporelle des signaux 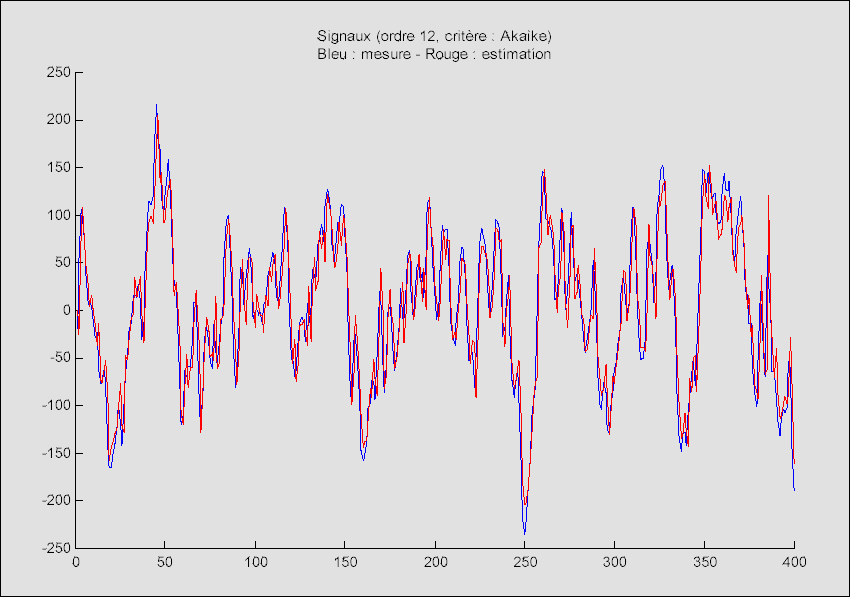
Représentation fréquentielle des signaux 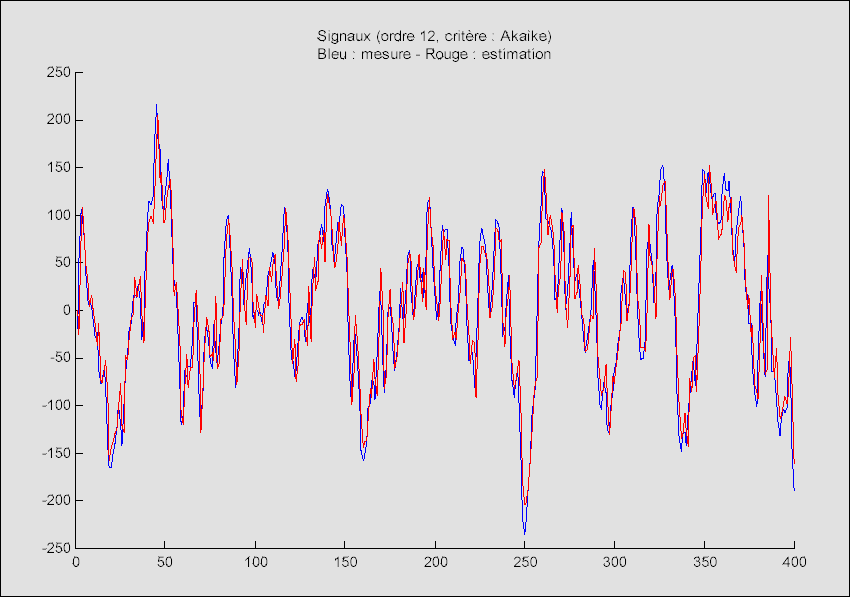
Représentation fréquentielle lissée des signaux
On remarque assez facilement que les deux signaux (la mesure et l'estimation par le modèle autorégressif) sont quasiment confondus. L'a priori sur le résultat du modèle autorégressif est donc vérifié : pour ce type de signaux (à composantes fréquentielles dominantes), le modèle autorégressif est satisfaisant.
Modèle moving average (MA)
Principe
Un modèle moving average est un filtre tout-zéro (composé uniquement de zéros) au travers duquel passe un bruit blanc. On détermine les coefficients de ce filtre tels que le signal à sa sortie soit le plus proche possible du signal à modéliser.
Fonction de transfert

La sortie d'un tel filtre dépend des échantillons précédents du bruit. Les coefficients bp(k) agissent uniquement sur ces derniers.
Fonction Matlab
La fonction suivante calcule les coefficients d'un modèle moving average en minimisant l'un des quatre critères donnés précédemment. Trois modes sont possibles :
Minimisation de l'erreur, choix de l'ordre
L'évolution de l'erreur est étudiée selon les quatre critères (premier mode de fonctionnement de la fonction).

Evolution des différents critères d'erreur
On remarque que pour ce type de signaux, l'erreur diverge fortement. Pour chacun de ces critère, l'ordre optimal est le même, mais l'erreur est plus importante que pour le modèle autorégressif.
Modélisation du signal EEG
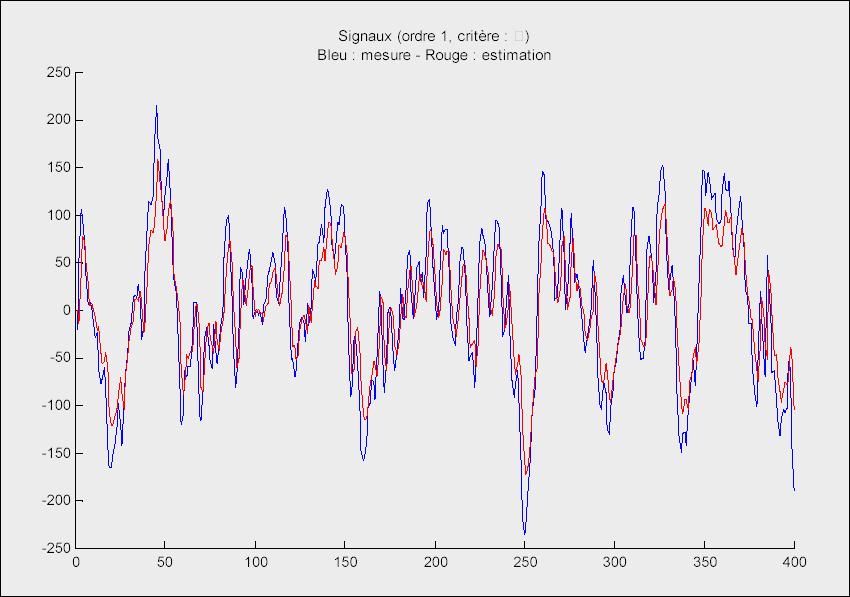
Représentation temporelle des signaux 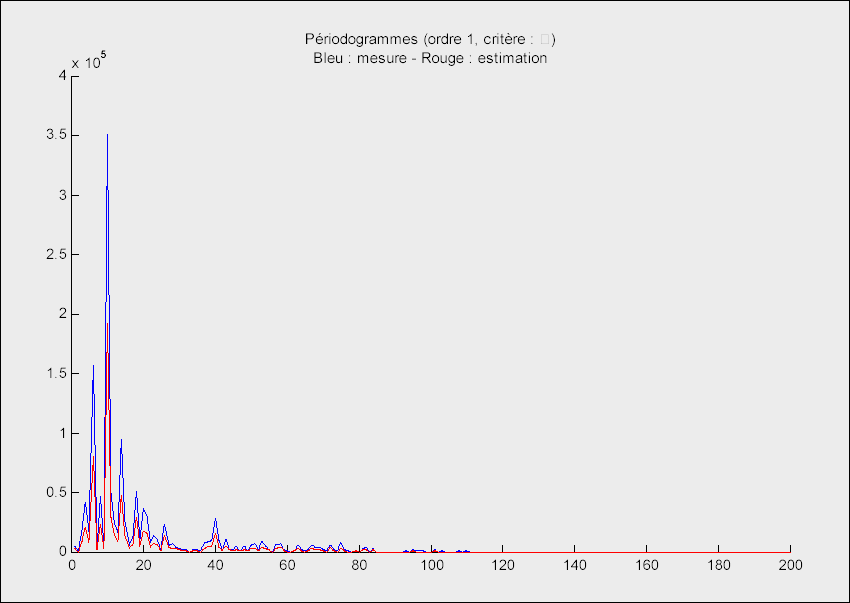
Représentation fréquentielle des signaux 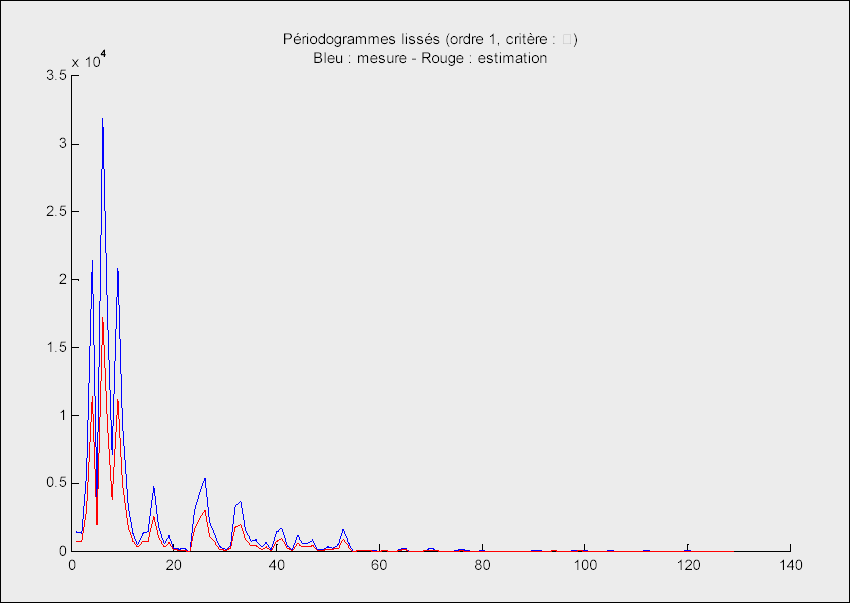
Représentation fréquentielle lissée des signaux
Conclusion
Ces techniques paramétriques sont très utiles dans les cas où le signal a des caractéristiques connues, souvent fréquentielles. Elles permettent une estimation assez simple et plutôt efficace du signal sans forcément en connaître la source et les modifications à y apporter. Le fait d'ignorer la provenance du signal permet de supposer qu'il a été généré par un bruit blanc passé à travers un filtre. Cette supposition permet de modéliser n'importe quel signal sans restriction, à condition de posséder quelques indications sur l'allure de son spectre. Elle offre également l'avantage d'être applicable à n'importe quel processus physique assimilable à un filtre.
| ||||
|
© S. NOBILI Pipo Prods. 2005 - Tous droits réservés Ce site respecte à la lettre les standards de l'Internet... Si vous rencontrez des problèmes de visualisation, vous devez vous poser des questions quant à la qualité de votre navigateur ! Ce site a été validé comme compatible avec les navigateurs suivants : Mozilla Firefox, Opera, Epiphany, Lynx et IE (je n'en avais pourtant pas trés envie...).  |